ARIMA

Posted on Edited on In

learn learn~~

Page

Stationarity and differencing

A stationary time series is one whose statistical properties such as mean, variance, autocorrelation, etc. are all constant over time. Most statistical forecasting methods are based on the assumption that the time series can be rendered approximately stationary (i.e., “stationarized”) through the use of mathematical transformations. A stationarized series is relatively easy to predict: you simply predict that its statistical properties will be the same in the future as they have been in the past! (Recall our famous forecasting quotes.) The predictions for the stationarized series can then be “untransformed,” by reversing whatever mathematical transformations were previously used, to obtain predictions for the original series. (The details are normally taken care of by your software.) Thus, finding the sequence of transformations needed to stationarize a time series often provides important clues in the search for an appropriate forecasting model. Stationarizing a time series through differencing (where needed) is an important part of the process of fitting an ARIMA model, as discussed in the ARIMA pages of these notes.

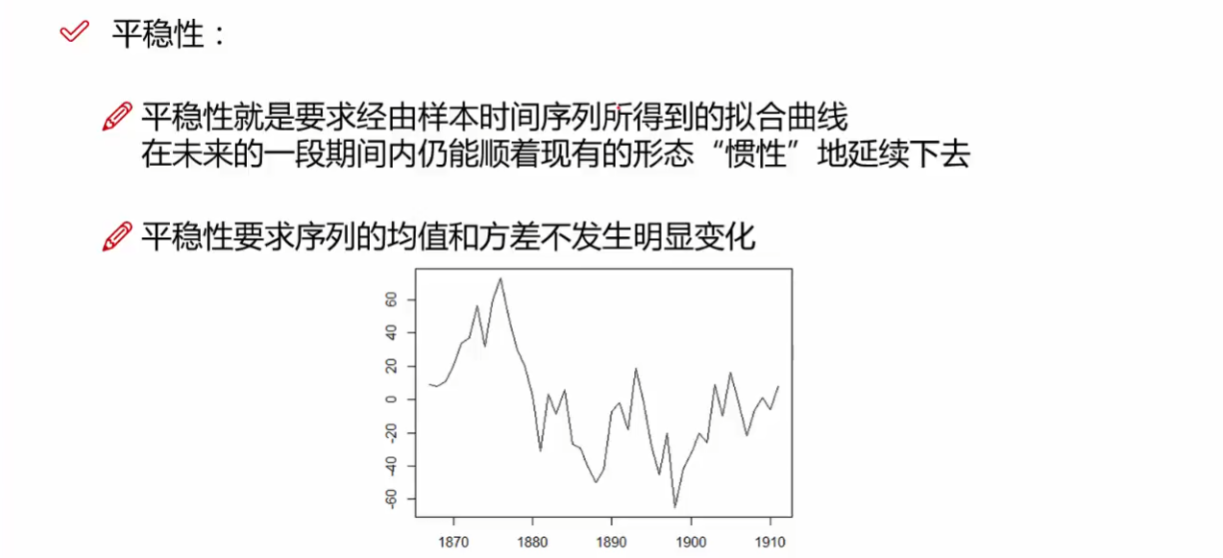
image-20220520120922114

image-20220520120547301

基本都是若平稳 严平稳不太现实

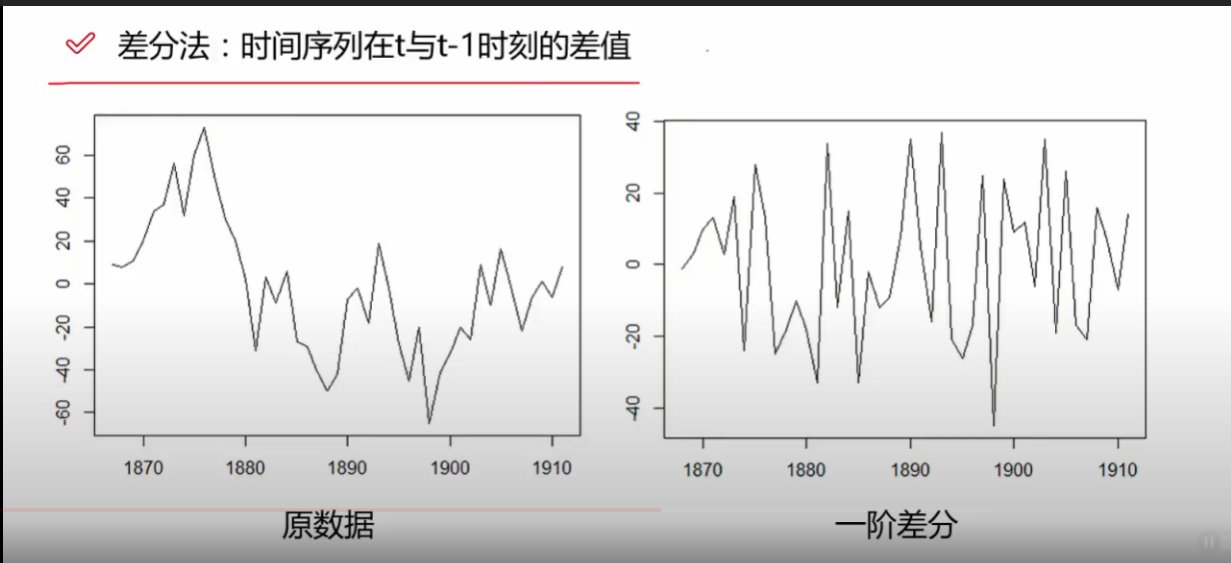
image-20220520120852730

差分法可以使得数据变得更加平稳

What does the p, d and q in ARIMA model mean

the value of d, therefore, is the minimum number of differencing needed to make the series stationary. And if the time series is already stationary, then d = 0.

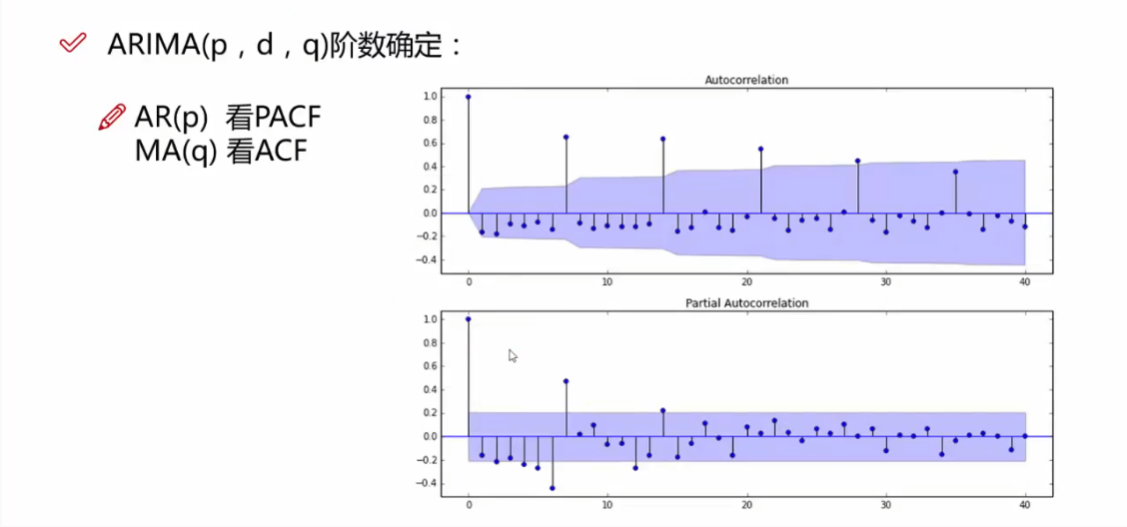
p is the order of the ‘Auto Regressive’ (AR) term. It refers to the number of lags of Y to be used as predictors. And q is the order of the ‘Moving Average’ (MA) term. It refers to the number of lagged forecast errors that should go into the ARIMA Model.

you can understand more clearly by reading next chapter

What are AR and MA models

AR

image-20220520121643408

限制

image-20220520122324677

MA

image-20220520122905060

AR+MA

image-20220520123101024

ARIMA

image-20220520123635421

what is ACF and PACF

ACF

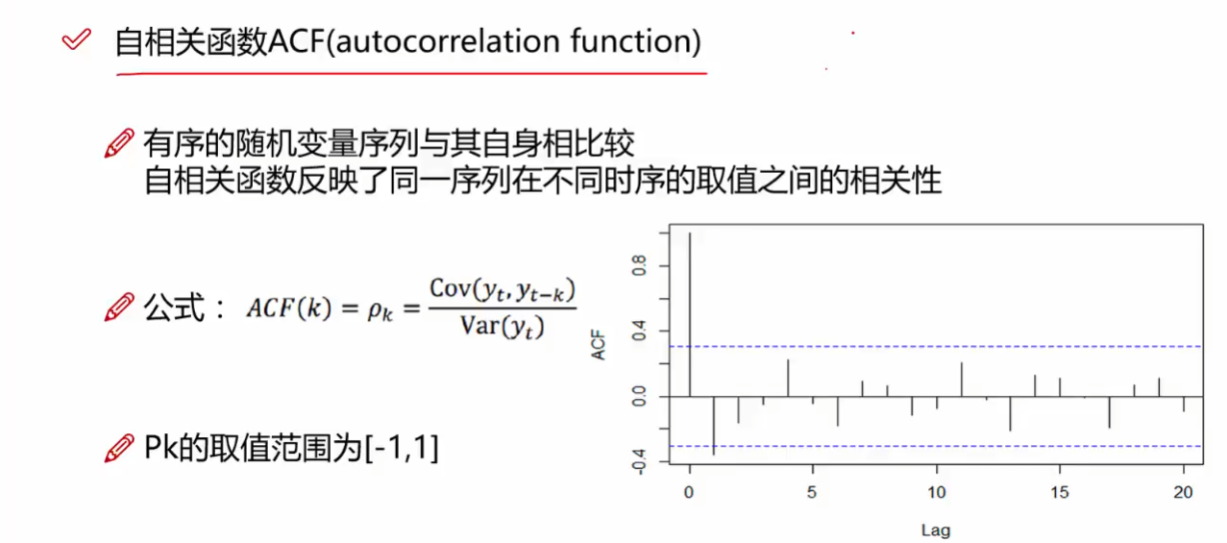
image-20220520123950209

PACF

单纯地考虑 x(t) 和 x(t-k) 的关系

image-20220520124724627

https://timeseriesreasoning.com/contents/partial-auto-correlation/

https://online.stat.psu.edu/stat510/lesson/2/2.2

How to find the order of the MA term (p,q,d)

image-20220520125414144

image-20220520131212749

How to find the order of differencing (d) in ARIMA model

The purpose of differencing it to make the time series stationary.

But you need to be careful to not over-difference the series. Because, an over differenced series may still be stationary, which in turn will affect the model parameters.

The right order of differencing is the minimum differencing required to get a near-stationary series which roams around a defined mean and the ACF plot reaches to zero fairly quick.

If the autocorrelations are positive for many number of lags (10 or more), then the series needs further differencing. On the other hand, if the lag 1 autocorrelation itself is too negative, then the series is probably over-differenced.

In the event, you can’t really decide between two orders of differencing, then go with the order that gives the least standard deviation in the differenced series.

check if the series is stationary using the Augmented Dickey Fuller test (adfuller()), from the statsmodels package.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np, pandas as pd
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt
plt.rcParams.update({'figure.figsize':(9,7), 'figure.dpi':120})

# Import data
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/wwwusage.csv', names=['value'], header=0)
# Original Series
fig, axes = plt.subplots(3, 2, sharex=True)
axes[0, 0].plot(df.value); axes[0, 0].set_title('Original Series')
plot_acf(df.value, ax=axes[0, 1] ,lags=np.arange(len(df) ))

# 1st Differencing
axes[1, 0].plot(df.value.diff()); axes[1, 0].set_title('1st Order Differencing')
plot_acf(df.value.diff().dropna(), ax=axes[1, 1], lags=np.arange(len(df) - 1))

# 2nd Differencing
axes[2, 0].plot(df.value.diff().diff()); axes[2, 0].set_title('2nd Order Differencing')
plot_acf(df.value.diff().diff().dropna(), ax=axes[2, 1],lags=np.arange(len(df) - 2))

plt.show()
111

​ (*)

1
2
3
4
5
from statsmodels.tsa.stattools import adfuller
from numpy import log
result = adfuller(df.value.dropna())
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])

we got

1
2
ADF Statistic: -2.464240
p-value: 0.124419

if P Value > 0.05 we go ahead with finding the order of differencing.

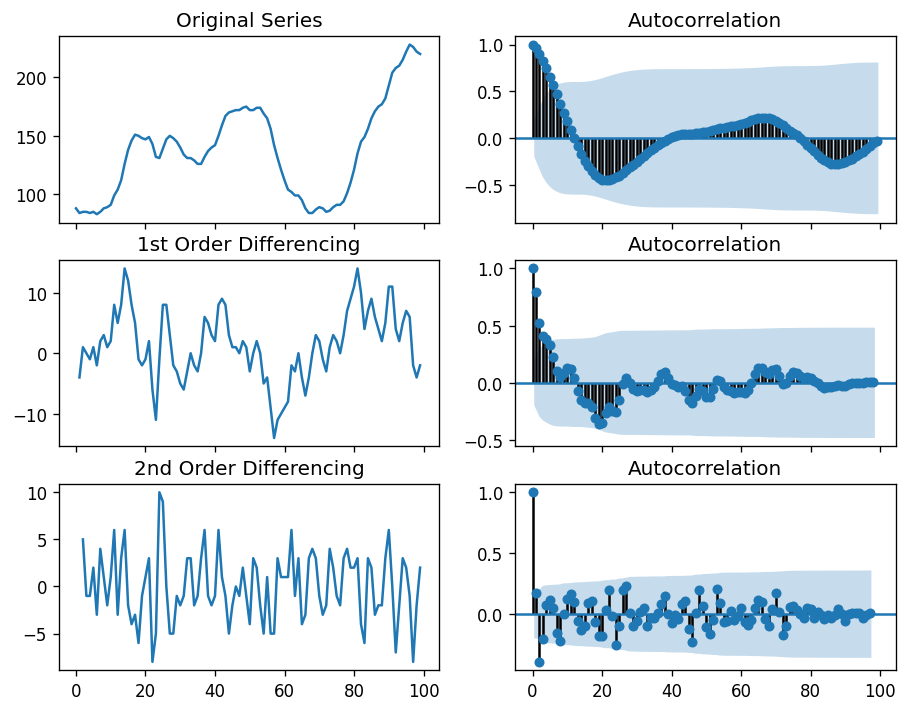
Since P-value is greater than the significance level, we difference the series. please look at picture (*).

For the above series, the time series reaches stationarity with two orders of differencing. But on looking at the autocorrelation plot for the 2nd differencing the lag goes into the far negative zone fairly quick, which indicates, the series might have been over differenced.

So, I am going to tentatively fix the order of differencing as 1 even though the series is not perfectly stationary (weak stationarity).

1
2
3
4
5
6
7
8
9
10
11
12
13
import pandas as pd
from pmdarima.arima.utils import ndiffs
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/wwwusage.csv', names=['value'], header=0)
y = df.value

## Adf Test
print(ndiffs(y, test='adf'))  # 2

# KPSS test
print(ndiffs(y, test='kpss'))  # 0

# PP test:
print(ndiffs(y, test='pp'))  # 2

ndiffs的文档–Number of differences required for a stationary series

How to find the order of the AR term (p)

How to find the order of the MA term (q)

（1）ACF和PACF 利用拖尾和截尾来确定(这里还是有点没太完全清楚，，，感觉我的判断和网上说的有点区别。。。反正代码可以自动找。。。)

（2）信息准则定阶（AIC、BIC、HQIC）

How to build the ARIMA Model

image-20220520131454425

1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np, pandas as pd  
from statsmodels.tsa.arima_model import ARIMA  
  
# importing data  
#https://raw.githubusercontent.com/selva86/datasets/master/austa.csv
#https://raw.githubusercontent.com/selva86/datasets/master/wwwusage.csv
mydata = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/wwwusage.csv', names = ['value'], header = 0)  
  
# Creating ARIMA model  
mymodel = ARIMA(mydata.value, order = (1, 1, 2))  
modelfit = mymodel.fit(disp = 0)  
print(modelfit.summary())

result:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
    ARIMA Model Results                              
==============================================================================
Dep. Variable:                D.value   No. Observations:                   99
Model:                 ARIMA(1, 1, 2)   Log Likelihood                -253.790
Method:                       css-mle   S.D. of innovations              3.119
Date:                Fri, 20 May 2022   AIC                            517.579
Time:                        11:59:24   BIC                            530.555
Sample:                             1   HQIC                           522.829
                                                                              
=================================================================================
                    coef    std err          z      P>|z|      [0.025      0.975]
---------------------------------------------------------------------------------
const             1.1202      1.290      0.868      0.387      -1.409       3.649
ar.L1.D.value     0.6351      0.257      2.469      0.015       0.131       1.139
ma.L1.D.value     0.5287      0.355      1.489      0.140      -0.167       1.224
ma.L2.D.value    -0.0010      0.321     -0.003      0.998      -0.631       0.629
                                    Roots                                    
=============================================================================
                  Real          Imaginary           Modulus         Frequency
-----------------------------------------------------------------------------
AR.1            1.5746           +0.0000j            1.5746            0.0000
MA.1           -1.8850           +0.0000j            1.8850            0.5000
MA.2          545.0568           +0.0000j          545.0568            0.0000
-----------------------------------------------------------------------------

The model summary reveals a lot of information. The table in the middle is the coefficients table where the values under ‘coef’ are the weights of the respective terms.

Notice here the coefficient of the MA2 term is close to zero and the P-Value in ‘P>|z|’ column is highly insignificant. It should ideally be less than 0.05 for the respective X to be significant.

So, let’s rebuild the model without the MA2 term.

1
2
3
4
# 1,1,1 ARIMA Model
model = ARIMA(df.value, order=(1,1,1))
model_fit = model.fit(disp=0)
print(model_fit.summary())

result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
    ARIMA Model Results                              
==============================================================================
Dep. Variable:                D.value   No. Observations:                   99
Model:                 ARIMA(1, 1, 1)   Log Likelihood                -253.790
Method:                       css-mle   S.D. of innovations              3.119
Date:                Fri, 20 May 2022   AIC                            515.579
Time:                        12:07:06   BIC                            525.960
Sample:                             1   HQIC                           519.779
                                                                              
=================================================================================
                    coef    std err          z      P>|z|      [0.025      0.975]
---------------------------------------------------------------------------------
const             1.1205      1.286      0.871      0.386      -1.400       3.641
ar.L1.D.value     0.6344      0.087      7.317      0.000       0.464       0.804
ma.L1.D.value     0.5297      0.089      5.932      0.000       0.355       0.705
                                    Roots                                    
=============================================================================
                  Real          Imaginary           Modulus         Frequency
-----------------------------------------------------------------------------
AR.1            1.5764           +0.0000j            1.5764            0.0000
MA.1           -1.8879           +0.0000j            1.8879            0.5000
-----------------------------------------------------------------------------

The model AIC has reduced, which is good. The P Values of the AR1 and MA1 terms have improved and are highly significant (<< 0.05).

Let’s plot the residuals to ensure there are no patterns (that is, look for constant mean and variance).

1
2
3
4
5
residuals = pd.DataFrame(model_fit.resid)
fig, ax = plt.subplots(1,2)
residuals.plot(title="Residuals", ax=ax[0])
residuals.plot(kind='kde', title='Density', ax=ax[1])
plt.show()

222

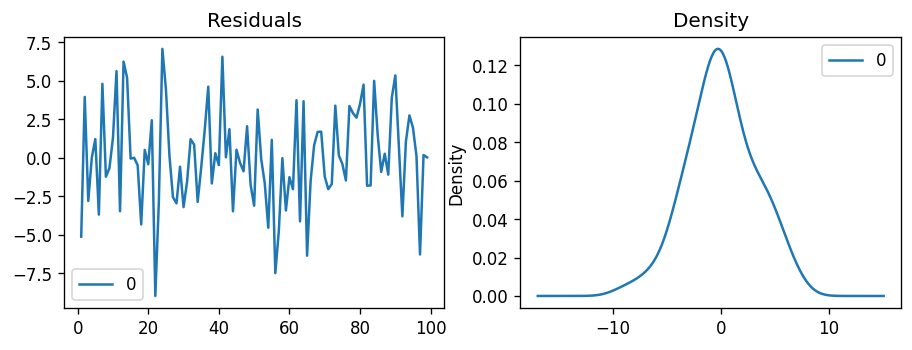
The residual errors seem fine with near zero mean and uniform variance. Let’s plot the actuals against the fitted values using plot_predict().

1
2
3
# Actual vs Fitted
model_fit.plot_predict(dynamic=False)
plt.show()

333

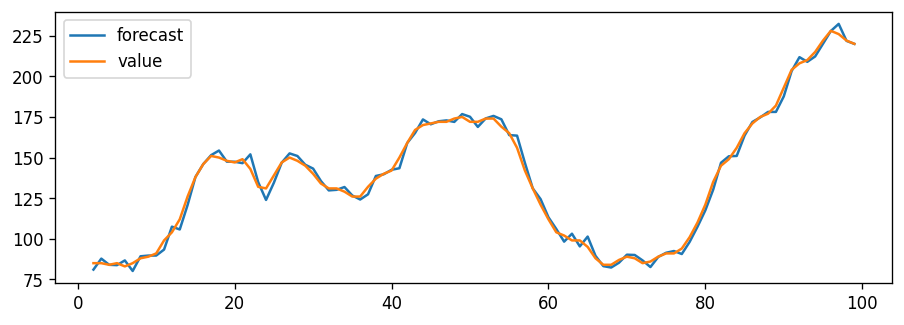
When you set dynamic=False the in-sample lagged values are used for prediction.

That is, the model gets trained up until the previous value to make the next prediction. This can make the fitted forecast and actuals look artificially good.

So, we seem to have a decent ARIMA model. But is that the best?

Can’t say that at this point because we haven’t actually forecasted into the future and compared the forecast with the actual performance.

So, the real validation you need now is the Out-of-Time cross-validation.

How to do find the optimal ARIMA model manually using Out-of-Time Cross validation

In Out-of-Time cross-validation, you take few steps back in time and forecast into the future to as many steps you took back. Then you compare the forecast against the actuals.

To do out-of-time cross-validation, you need to create the training and testing dataset by splitting the time series into 2 contiguous parts in approximately 75:25 ratio or a reasonable proportion based on time frequency of series.

Why am I not sampling the training data randomly you ask?

That’s because the order sequence of the time series should be intact in order to use it for forecasting.

1
2
3
4
5
from statsmodels.tsa.stattools import acf

# Create Training and Test
train = df.value[:85]
test = df.value[85:]

we can now build the ARIMA model on training dataset, forecast and plot it.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Build Model
# model = ARIMA(train, order=(3,2,1))  
model = ARIMA(train, order=(1, 1, 1))  
fitted = model.fit(disp=-1)  

# Forecast
fc, se, conf = fitted.forecast(15, alpha=0.05)  # 95% conf

# Make as pandas series
fc_series = pd.Series(fc, index=test.index)
lower_series = pd.Series(conf[:, 0], index=test.index)
upper_series = pd.Series(conf[:, 1], index=test.index)

# Plot
plt.figure(figsize=(12,5), dpi=100)
plt.plot(train, label='training')
plt.plot(test, label='actual')
plt.plot(fc_series, label='forecast')
plt.fill_between(lower_series.index, lower_series, upper_series, 
                 color='k', alpha=.15)
plt.title('Forecast vs Actuals')
plt.legend(loc='upper left', fontsize=8)
plt.show()

555

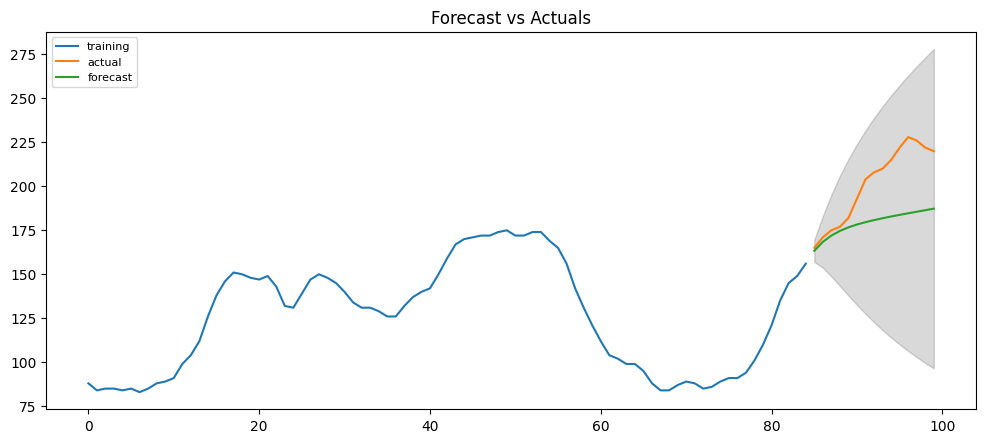
From the chart, the ARIMA(1,1,1) model seems to give a directionally correct forecast. And the actual observed values lie within the 95% confidence band. That seems fine.

But each of the predicted forecasts is consistently below the actuals. That means, by adding a small constant to our forecast, the accuracy will certainly improve. So, there is definitely scope for improvement.

So, what I am going to do is to increase the order of differencing to two, that is set d=2 and iteratively increase p to up to 5 and then q up to 5 to see which model gives least AIC and also look for a chart that gives closer actuals and forecasts.

While doing this, I keep an eye on the P values of the AR and MA terms in the model summary. They should be as close to zero, ideally, less than 0.05.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Build Model
model = ARIMA(train, order=(3, 2, 1))  
fitted = model.fit(disp=-1)  
print(fitted.summary())

# Forecast
fc, se, conf = fitted.forecast(15, alpha=0.05)  # 95% conf

# Make as pandas series
fc_series = pd.Series(fc, index=test.index)
lower_series = pd.Series(conf[:, 0], index=test.index)
upper_series = pd.Series(conf[:, 1], index=test.index)

# Plot
plt.figure(figsize=(12,5), dpi=100)
plt.plot(train, label='training')
plt.plot(test, label='actual')
plt.plot(fc_series, label='forecast')
plt.fill_between(lower_series.index, lower_series, upper_series, 
                 color='k', alpha=.15)
plt.title('Forecast vs Actuals')
plt.legend(loc='upper left', fontsize=8)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
         ARIMA Model Results                              
==============================================================================
Dep. Variable:               D2.value   No. Observations:                   83
Model:                 ARIMA(3, 2, 1)   Log Likelihood                -214.248
Method:                       css-mle   S.D. of innovations              3.153
Date:                Fri, 20 May 2022   AIC                            440.497
Time:                        12:22:22   BIC                            455.010
Sample:                             2   HQIC                           446.327
                                                                              
==================================================================================
                     coef    std err          z      P>|z|      [0.025      0.975]
----------------------------------------------------------------------------------
const              0.0483      0.084      0.577      0.565      -0.116       0.212
ar.L1.D2.value     1.1386      0.109     10.399      0.000       0.924       1.353
ar.L2.D2.value    -0.5923      0.155     -3.827      0.000      -0.896      -0.289
ar.L3.D2.value     0.3079      0.111      2.778      0.007       0.091       0.525
ma.L1.D2.value    -1.0000      0.035    -28.799      0.000      -1.068      -0.932
                                    Roots                                    
=============================================================================
                  Real          Imaginary           Modulus         Frequency
-----------------------------------------------------------------------------
AR.1            1.1557           -0.0000j            1.1557           -0.0000
AR.2            0.3839           -1.6318j            1.6763           -0.2132
AR.3            0.3839           +1.6318j            1.6763            0.2132
MA.1            1.0000           +0.0000j            1.0000            0.0000
-----------------------------------------------------------------------------

The AIC has reduced to 440 from 515. Good. The P-values of the X terms are less the < 0.05, which is great.

So overall it’s much better.

Ideally, you should go back multiple points in time, like, go back 1, 2, 3 and 4 quarters and see how your forecasts are performing at various points in the year.

Here’s a great practice exercise: Try to go back 27, 30, 33, 36 data points and see how the forcasts performs. The forecast performance can be judged using various accuracy metrics discussed next.

Accuracy Metrics for Time Series Forecast

The commonly used accuracy metrics to judge forecasts are:

  1. Mean Absolute Percentage Error (MAPE)
  2. Mean Error (ME)
  3. Mean Absolute Error (MAE)
  4. Mean Percentage Error (MPE)
  5. Root Mean Squared Error (RMSE)
  6. Lag 1 Autocorrelation of Error (ACF1)
  7. Correlation between the Actual and the Forecast (corr)
  8. Min-Max Error (minmax)

Typically, if you are comparing forecasts of two different series, the MAPE, Correlation and Min-Max Error can be used.

Why not use the other metrics?

Because only the above three are percentage errors that vary between 0 and 1. That way, you can judge how good is the forecast irrespective of the scale of the series.

The other error metrics are quantities. That implies, an RMSE of 100 for a series whose mean is in 1000’s is better than an RMSE of 5 for series in 10’s. So, you can’t really use them to compare the forecasts of two different scaled time series.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Accuracy metrics
def forecast_accuracy(forecast, actual):
    mape = np.mean(np.abs(forecast - actual)/np.abs(actual))  # MAPE
    me = np.mean(forecast - actual)             # ME
    mae = np.mean(np.abs(forecast - actual))    # MAE
    mpe = np.mean((forecast - actual)/actual)   # MPE
    rmse = np.mean((forecast - actual)**2)**.5  # RMSE
    corr = np.corrcoef(forecast, actual)[0,1]   # corr
    mins = np.amin(np.hstack([forecast[:,None], 
                              actual[:,None]]), axis=1)
    maxs = np.amax(np.hstack([forecast[:,None], 
                              actual[:,None]]), axis=1)
    minmax = 1 - np.mean(mins/maxs)             # minmax
    acf1 = acf(fc-test)[1]                      # ACF1
    return({'mape':mape, 'me':me, 'mae': mae, 
            'mpe': mpe, 'rmse':rmse, 'acf1':acf1, 
            'corr':corr, 'minmax':minmax})

forecast_accuracy(fc, test.values)

#> {'mape': 0.02250131357314834,
#>  'me': 3.230783108990054,
#>  'mae': 4.548322194530069,
#>  'mpe': 0.016421001932706705,
#>  'rmse': 6.373238534601827,
#>  'acf1': 0.5105506325288692,
#>  'corr': 0.9674576513924394,
#>  'minmax': 0.02163154777672227}

Around 2.2% MAPE implies the model is about 97.8% accurate in predicting the next 15 observations.

Now you know how to build an ARIMA model manually.

But in industrial situations, you will be given a lot of time series to be forecasted and the forecasting exercise be repeated regularly.

So we need a way to automate the best model selection process.

How to do Auto Arima Forecast in Python

Like R’s popular auto.arima() function, the pmdarima package provides auto_arima() with similar functionality.

auto_arima() uses a stepwise approach to search multiple combinations of p,d,q parameters and chooses the best model that has the least AIC.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from statsmodels.tsa.arima_model import ARIMA
import pmdarima as pm
import pandas as pd

df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/wwwusage.csv', names=['value'], header=0)

model = pm.auto_arima(df.value, start_p=1, start_q=1,
                      test='adf',       # use adftest to find optimal 'd'
                      max_p=3, max_q=3, # maximum p and q
                      m=1,              # frequency of series
                      d=None,           # let model determine 'd'
                      seasonal=False,   # No Seasonality
                      start_P=0, 
                      D=0, 
                      trace=True,
                      error_action='ignore',  
                      suppress_warnings=True, 
                      stepwise=True)

print(model.summary())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
Performing stepwise search to minimize aic
 ARIMA(1,2,1)(0,0,0)[0] intercept   : AIC=525.587, Time=0.21 sec
 ARIMA(0,2,0)(0,0,0)[0] intercept   : AIC=533.474, Time=0.01 sec
 ARIMA(1,2,0)(0,0,0)[0] intercept   : AIC=532.437, Time=0.04 sec
 ARIMA(0,2,1)(0,0,0)[0] intercept   : AIC=525.893, Time=0.09 sec
 ARIMA(0,2,0)(0,0,0)[0]             : AIC=531.477, Time=0.03 sec
 ARIMA(2,2,1)(0,0,0)[0] intercept   : AIC=515.248, Time=0.20 sec
 ARIMA(2,2,0)(0,0,0)[0] intercept   : AIC=513.459, Time=0.18 sec
 ARIMA(3,2,0)(0,0,0)[0] intercept   : AIC=515.284, Time=0.16 sec
 ARIMA(3,2,1)(0,0,0)[0] intercept   : AIC=inf, Time=1.25 sec
 ARIMA(2,2,0)(0,0,0)[0]             : AIC=511.465, Time=0.14 sec
 ARIMA(1,2,0)(0,0,0)[0]             : AIC=530.444, Time=0.09 sec
 ARIMA(3,2,0)(0,0,0)[0]             : AIC=513.291, Time=0.32 sec
 ARIMA(2,2,1)(0,0,0)[0]             : AIC=513.256, Time=0.33 sec
 ARIMA(1,2,1)(0,0,0)[0]             : AIC=523.592, Time=0.19 sec
 ARIMA(3,2,1)(0,0,0)[0]             : AIC=inf, Time=1.68 sec

Best model:  ARIMA(2,2,0)(0,0,0)[0]          
Total fit time: 4.991 seconds
                               SARIMAX Results                                
==============================================================================
Dep. Variable:                      y   No. Observations:                  100
Model:               SARIMAX(2, 2, 0)   Log Likelihood                -252.732
Date:                Fri, 20 May 2022   AIC                            511.465
Time:                        12:29:31   BIC                            519.220
Sample:                             0   HQIC                           514.601
                                - 100                                         
Covariance Type:                  opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ar.L1          0.2579      0.103      2.510      0.012       0.056       0.459
ar.L2         -0.4407      0.087     -5.093      0.000      -0.610      -0.271
sigma2        10.1268      1.519      6.668      0.000       7.150      13.103
===================================================================================
Ljung-Box (L1) (Q):                   0.05   Jarque-Bera (JB):                 0.10
Prob(Q):                              0.82   Prob(JB):                         0.95
Heteroskedasticity (H):               0.49   Skew:                            -0.07
Prob(H) (two-sided):                  0.05   Kurtosis:                         2.92
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

I met a bug here

1
2
3
4
5
6
7
ARIMA(3,2,1)(0,0,0)[0] intercept   : AIC=inf, Time=1.25 sec
ARIMA(2,2,0)(0,0,0)[0]             : AIC=511.465, Time=0.14 sec
ARIMA(1,2,0)(0,0,0)[0]             : AIC=530.444, Time=0.09 sec
ARIMA(3,2,0)(0,0,0)[0]             : AIC=513.291, Time=0.32 sec
ARIMA(2,2,1)(0,0,0)[0]             : AIC=513.256, Time=0.33 sec
ARIMA(1,2,1)(0,0,0)[0]             : AIC=523.592, Time=0.19 sec
ARIMA(3,2,1)(0,0,0)[0]             : AIC=inf, Time=1.68 sec

why AIC == inf ?

How to build SARIMAX Model with exogenous variable

https://raw.githubusercontent.com/selva86/datasets/master/a10.csv

1
2
# Import Data
data = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Compute Seasonal Index
from statsmodels.tsa.seasonal import seasonal_decompose
from dateutil.parser import parse

# multiplicative seasonal component
result_mul = seasonal_decompose(data['value'][-36:],   # 3 years
                                model='multiplicative', 
                                extrapolate_trend='freq')

seasonal_index = result_mul.seasonal[-12:].to_frame()
seasonal_index['month'] = pd.to_datetime(seasonal_index.index).month

# merge with the base data
data['month'] = data.index.month
df = pd.merge(data, seasonal_index, how='left', on='month')
df.columns = ['value', 'month', 'seasonal_index']
df.index = data.index  # reassign the index.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
import pmdarima as pm

# SARIMAX Model
sxmodel = pm.auto_arima(df[['value']], exogenous=df[['seasonal_index']],
                           start_p=1, start_q=1,
                           test='adf',
                           max_p=3, max_q=3, m=12,
                           start_P=0, seasonal=True,
                           d=None, D=1, trace=True,
                           error_action='ignore',  
                           suppress_warnings=True, 
                           stepwise=True)

sxmodel.summary()

https://zhuanlan.zhihu.com/p/157960700

https://stackoverflow.com/questions/44235558/statespace-sarimax-model-why-the-model-use-all-the-data-to-train-mode-and-pred

https://analyticsindiamag.com/complete-guide-to-sarimax-in-python-for-time-series-modeling/

bug

https://stats.stackexchange.com/questions/160612/auto-arima-doesnt-calculate-aic-values-for-the-majority-of-models

tips

parameter

https://alkaline-ml.com/pmdarima/tips_and_tricks.html

How to decide m?

In my code, maybe I need to set m = 7.

  • 7 - daily
  • 12 - monthly
  • 52 - weekly

let’s take a look at one question

I have two large time series data. One is separated by seconds intervals and the other by minutes. The length of each time series is 180 days. I’m using R (3.1.1) for forecasting the data. I’d like to know the value of the “frequency” argument in the ts() function in R, for each data set. Since most of the examples and cases I’ve seen so far are for months or days at the most, it is quite confusing for me when dealing with equally separated seconds or minutes. According to my understanding, the “frequency” argument is the number of observations per season. So what is the “season” in the case of seconds/minutes? My guess is that since there are 86,400 seconds and 1440 minutes a day, these should be the values for the “freq” argument. Is that correct?

Yes, the “frequency”is the number of observations per “cycle” (normally a year, but sometimes a week, a day or an hour). This is the opposite of the definition of frequency in physics, or in Fourier analysis, where “period” is the length of the cycle, and “frequency” is the inverse of period. When using the ts() function in R, the following choices should be used.

Data Frequency
Annual 1
Quarterly 4
Monthly 12
Weekly 52

Actually, there are not 52 weeks in a year, but 365.25/7 = 52.18 on average, allowing for a leap year every fourth year. But most functions which use ts objects require integer frequency.

If the frequency of observations is greater than once per week, then there is usually more than one way of handling the frequency. For example, data with daily observations might have a weekly seasonality (frequency=7) or an annual seasonality (frequency=365.25). Similarly, data that are observed every minute might have an hourly seasonality (frequency=60), a daily seasonality (frequency=24x60=1440), a weekly seasonality (frequency=24x60x7=10080) and an annual seasonality (frequency=24x60x365.25=525960). If you want to use a ts object, then you need to decide which of these is the most important.

An alternative is to use a msts object (defined in the forecast package) which handles multiple seasonality time series. Then you can specify all the frequencies that might be relevant. It is also flexible enough to handle non-integer frequencies.

Frequencies
Data Minute Hour Day Week Year
Daily 7 365.25
Hourly 24 168 8766
Half-hourly 48 336 17532
Minutes 60 1440 10080 525960
Seconds 60 3600 86400 604800 31557600

You won’t necessarily want to include all of these frequencies — just the ones that are likely to be present in the data. For example, any natural phenomena (e.g., sunshine hours) is unlikely to have a weekly period, and if your data are measured in one-minute intervals over a 3 month period, there is no point including an annual frequency.

For example, the taylor data set from the forecast package contains half-hourly electricity demand data from England and Wales over about 3 months in 2000. It was defined as

1
taylor <- msts(x, seasonal.periods=c(48,336)

One convenient model for multiple seasonal time series is a TBATS model:

1
2
taylor.fit <- tbats(taylor)
plot(forecast(taylor.fit))

(Warning: this takes a few minutes.)

If an msts object is used with a function designed for ts objects, the largest seasonal period is used as the “frequency” attribute.

Some ideas and questions?

  • The ARIMA model seems to process good result for short-term forecasting, but it is difficult to get results in the long-term prediction. So it seems unconvincing to use the ARIMA model as a comparative experiment in long-term forecasting?
  • In my experiments, I found that a more accurate setting of the seasonal(parameter m) resulted in increased training time and made it difficult for my experiments to continue.

reference

https://otexts.com/fpp2/stationarity.html

https://people.duke.edu/~rnau/411home.htm

https://www.machinelearningplus.com/time-series/arima-model-time-series-forecasting-python/

https://www.youtube.com/watch?v=ikkOBWQj9X8

https://www.machinelearningplus.com/time-series/augmented-dickey-fuller-test/

https://robjhyndman.com/hyndsight/seasonal-periods/

https://alkaline-ml.com/pmdarima/modules/generated/pmdarima.arima.auto_arima.html

https://zhuanlan.zhihu.com/p/157960700