run哥带你手撕全连接层

Posted on 2022-05-26 Edited on 2023-03-28 In run哥带你手撕系列

学！

what is fully-connected layers?

Fully-connected layers, also known as linear layers, connect every input neuron to every output neuron and are commonly used in neural networks.

Figure 1. Example of a small fully-connected layer with four input and eight output neurons.

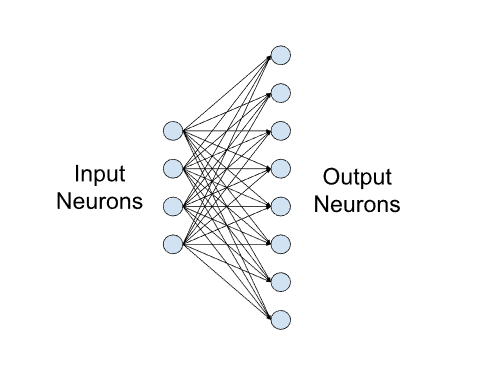
Fully Connected 可以看作一个转换矩阵把 feature matrix 到Label space

但是只用一层fully connected layer 有时候没法解决非线性问题

而如果有两层或以上fully connected layer就可以很好地解决非线性问题了

等价于问你卷积层和全连接层的区别

全连接层

所以全连接层有三个特点：

关注全局信息（每个点都和前后层的所有点链接）

参数量巨大，计算耗时

输入维度需要匹配（因为是矩阵运算，维度不一致无法计算）

卷积层

局部链接：当前层的神经元只和下一层神经元的局部链接（并不是全连接层的全局链接）

权重共享：神经元的参数（如上图的3*3卷积核），在整个特征图上都是共享的，而不是每个滑动窗口都不同

也正是因为这两个特性，所以卷积层相比于全连接层有如下优点：

需要学习的参数更少，从而降低了过度拟合的可能性，因为该模型不如完全连接的网络复杂。

只需要考虑中的上下文/共享信息。这个未来在许多应用中非常重要，例如图像、视频、文本和语音处理/挖掘，因为相邻输入（例如像素、帧、单词等）通常携带相关信息。

但需要注意的是，无论是全连接层，还是卷积层，都是线性层，只能拟合线性函数，所以都需要通过ReLU等引入非线性，以增加模型的表达能力。比如ReLU函数接受一个输入x，并返回{0, x}的最大值。ReLU(x) = argmax(x, 0)。

一种简单的防止过拟合的方法

典型的神经网络训练过程是将输入通过网络进行正向传导，然后将误差进行反向传播，dropout在这个过程中，网络中的节点以概率p被随机丢弃，本次训练中，被丢弃的节点不再起作用，但是接下来的训练中，之前的“丢弃”节点可能继续被“丢弃”，也可能加入训练。

（p一般设置为0.5，也可以根据模型的过拟合风险情况调整，加大或者减小）

参考着看知乎嘛不能全信