智能控制原理实践

Posted on 2022-06-22 Edited on 2023-03-14 In 考试

最近期末啥都要学记录一下很多东西直接搬运

HW1 – 设计模糊控制器，并与PID控制效果相比较

模糊控制

模糊控制的基本原理

模糊控制是以模糊集理论、模糊语言变量和模糊逻辑推理为基础的一种智能控制方法，它是从行为上模仿人的模糊推理和决策过程的一种智能控制方法。该方法首先将操作人员或专家经验编成模糊规则，然后将来自传感器的实时信号模糊化，将模糊化后的信号作为模糊规则的输入，完成模糊推理，将推理后得到的输出量加到执行器上。

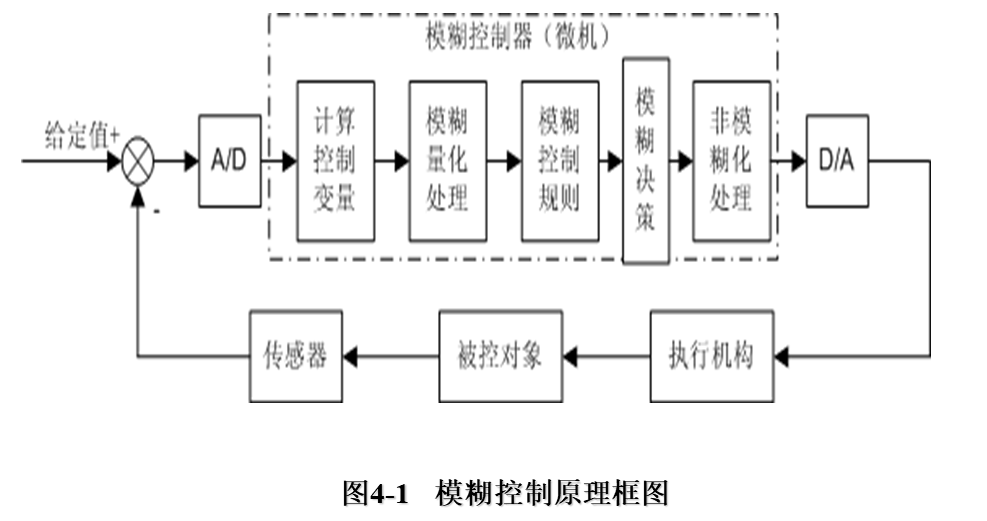
模糊控制器

模糊控制器（Fuzzy Controller—FC）：也称为模糊逻辑控制器（Fuzzy Logic Controller—FLC）,由于所采用的模糊控制规则是由模糊理论中模糊条件语句来描述的，因此模糊控制器是一种语言型控制器，故也称为模糊语言控制器（Fuzzy Language Controller—FLC）。

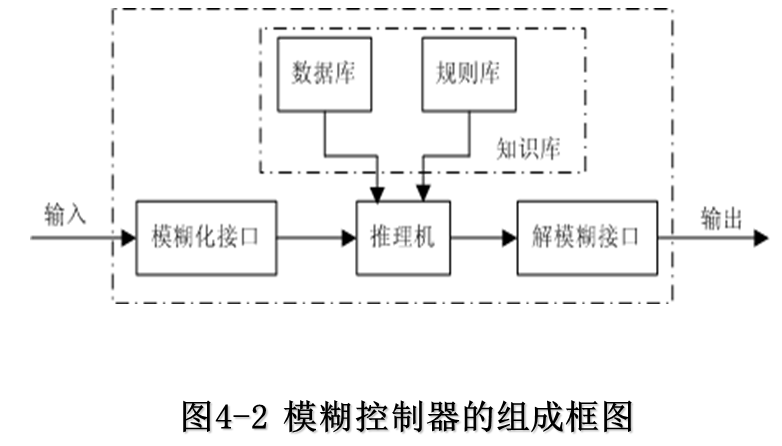
模糊化接口（Fuzzy interface）

模糊控制器的输入必须通过模糊化才能用于控制输出的求解，因此它实际上是模糊控制器的输入接口。它的主要作用是将真实的确定量输入转换为一个模糊矢量。
知识库（Knowledge Base—KB）

知识库由数据库和规则库两部分构成。

①数据库（Data Base—DB）数据库所存放的是所有输入、输出变量的全部模糊子集的隶属度矢量值（即经过论域等级离散化以后对应值的集合），若论域为连续域则为隶属度函数。在规则推理的模糊关系方程求解过程中，向推理机提供数据。

②规则库（Rule Base—RB）模糊控制器的规则司基于专家知识或手动操作人员长期积累的经验，它是按人的直觉推理的一种语言表示形式。模糊规则通常有一系列的关系词连接而成，如if-then、else、also、end、or等，关系词必须经过“翻译”才能将模糊规则数值化。最常用的关系词为if-then、also，对于多变量模糊控制系统，还有and等。

推理与解模糊接口（Inference and Defuzzy-interface）

推理是模糊控制器中，根据输入模糊量，由模糊控制规则完成模糊推理来求解模糊关系方程，并获得模糊控制量的功能部分。在模糊控制中，考虑到推理时间，通常采用运算较简单的推理方法。最基本的有Zadeh近似推理，它包含有正向推理和逆向推理两类。正向推理常被用于模糊控制中，而逆向推理一般用于知识工程学领域的专家系统中。推理结果的获得，表示模糊控制的规则推理功能已经完成。但是，至此所获得的结果仍是一个模糊矢量，不能直接用来作为控制量，还必须作一次转换，求得清晰的控制量输出，即为解模糊。通常把输出端具有转换功能作用的部分称为解模糊接口。

PID控制

前置知识

PID控制是业内最常见的控制算法，在工业控制领域有很高的接受度。 PID控制器的广泛应用，得益于其在多种操作条件下稳定的性能，以及易操作的特性。工程师可以用简单直观的方式实现PID控制。

PID控制有三个基本要件：比例(proportional)、积分(integral)、微分(derivative)。通过这三种不同的计算方法获取最优化的结果。

先了解一下闭环系统及其相关术语

闭环系统
在一个典型的控制系统里，过程变量是需要被控制的系统变量。例如，温度(ºC)、压强(psi)、流速(升/分钟)。传感器用来测量过程变量，并对控制系统做出反馈。 设定值是过程变量的期望值或必须达到的值。例如，在一个温控系统中，设定温度值为100摄氏度。在任意时间点上，控制系统算法（补偿器）使用过程变量和设定值之间的差值，得到期望的激励器输出，驱动系统（设备）。例如，如测量得到的温度过程变量为100 ºC，期望的温度设定值为120 ºC，控制器算法的激励器输出将指示打开加热器。打开加热器，整个系统就逐渐变热，温度过程变量测得的结果也会增加。这就是一个闭环控制系统，读取传感器，提供即时反馈，计算期望的激励器输出，这三项操作以固定速率循环往复，如图1所示。

在很多情况下，激励器输出不是对系统有影响的唯一信号。例如，在温度舱内，可能会有冷空气源。冷空气吹入舱内时，会扰动环境温度。这类扰动因素叫做干扰。设计控制系统时，通常会尽可能减少对过程变量的干扰因素。

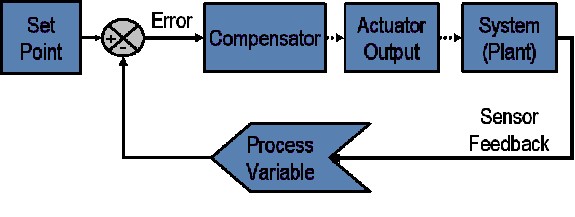
图1：典型闭环系统的示意图

术语定义
控制设计过程从定义性能需求开始。控制系统的性能一般通过应用一个阶跃函数作为设定值命令变量，然后测量过程变量的响应。一般来说，通过测量定义的波形特征来量化响应。上升时间是系统从稳定状态（或最终值）的10%上升到90%所需的时间。过冲百分比是过程变量超过最终值的百分比数，以最终值的百分比表示。稳定时间是过程变量值稳定在最终值5%范围内所需的时间。稳定状态误差是过程变量和设定值之间的差值。这些值的确切定义在学术和工业上的定义不尽相同。

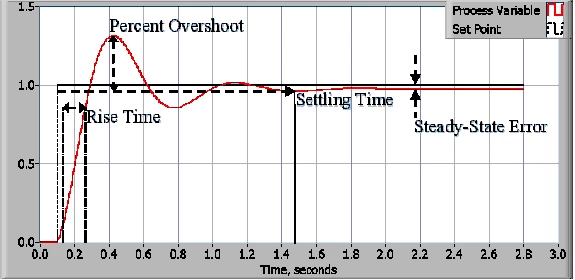
图2：典型闭环系统的响应

使用这些量来定义控制系统的性能要求时，需定义控制系统满足这些需求时可能遇到的“最坏情况”。一般而言，系统中都有一个影响过程变量或过程变量测量值的干扰。所以，要设计一个在最坏情况下都能满意工作的控制系统。控制系统克服干扰的能力，被称为控制系统的干扰抑制。

在某些情况下，对于一个给定控制输出的系统反馈可能会因时间变化。在非线性系统中，控制参数在某个时刻给出的期望响应，但是在另一个时刻可能无法给出满意的响应。例如，舱室中几乎为空时，其对加热器输出的响应比舱室填满或几乎填满液体时更快。控制系统对干扰和非线性的耐受度，被称为控制系统的稳定性。

有些系统会出现非预期的不响应期。不响应期是过程变量改变和观测到该改变之间的时间延迟。例如，如温度传感器离冷水阀较远，传感器无法立即监测到冷水阀打开或关闭。不响应期也可能是因为系统或输出激励器响应控制命令比较缓慢。例如，阀门打开和关闭的速度很缓慢。在化工厂，造成不响应期的常见原因是化学试剂在管道中流通需要时间。

循环周期也是闭环系统的重要参数。调用控制算法之间的时间间隔是循环周期时间。变化迅速或操作复杂的系统，需要更快的循环速率。

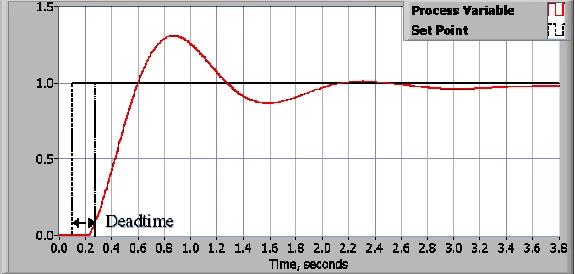
图3：闭环系统的响应及其不响应期

一旦指定了性能需求，即可开始检查系统并选择合适的控制方案。在大多数应用中，PID控制程序必须提供结果。

PID理论

比例响应
比例模块取决于设定值和过程变量之间的差值。这个差值被称为“误差”。 比例增益 *(Kc)*决定了输出响应对误差信号的比例。例如，误差为10，比例增益为5时，比例响应为50。一般而言，提高比例增益会增加控制系统响应的速度。但是，如果比例增益太大，过程变量会有振荡。如果继续增加Kc，系统振荡会越来越大，以至于超出控制，使得系统变得不稳定。

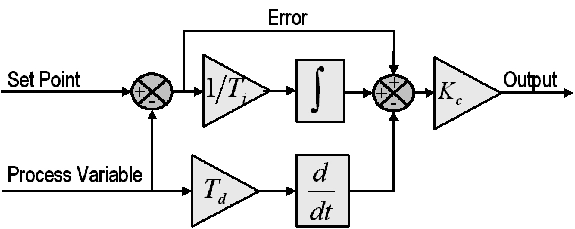
图4：基本PID控制算法的示意图

积分响应
积分模块将一段时间内的误差相加。即使是一个很小的误差，也会让积分响应缓慢增加。积分响应会根据时间持续增加，除非误差为0。积分响应的目的在于将稳定状态的误差保持在0。稳定状态误差是过程变量和设定值之间的差值。当积分操作满足了控制器的条件，而控制器还未将误差保持在0时，会产生积分饱和的结果。

微分响应
微分模块在过程变量迅速增大时停止输出。微分响应与过程变量变化的速度之间成比例关系。增加*微分时间(Td)*会使控制系统对误差的反应更加剧烈，会增加整个控制系统的响应时间。大多数实用控制系统使用非常小的微分时间(Td)，因为微分响应对过程变量的噪声特别敏感。如传感器反馈信号中有噪声或控制循环速率太低，微分响应会使控制系统变得不稳定。

作业

有被控对象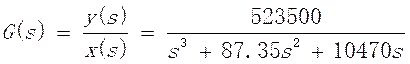，在MATLAB环境下设计模糊控制器，并与PID控制效果相比较。报告中要列出模糊控制规则表，模糊控制器各个输入输出量的隶属函数名称、论域、类型、参数。采用M文件或者SIMULINK实现均可。

HW3 – 用遗传算法优化PID控制器参数

用遗传算法优化PID控制器参数。有被控对象，设计遗传算法对PID控制器参数进行优化，采用二进制编码

遗传算法学习（only copy）

简述

遗传算法（Genetic Algorithm, GA）起源于对生物系统所进行的计算机模拟研究。它是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，借鉴了达尔文的进化论和孟德尔的遗传学说。其本质是一种高效、并行、全局搜索的方法，能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最佳解。

概念

遗传算法中每一条染色体，对应着遗传算法的一个解决方案，一般我们用适应性函数（fitness function）来衡量这个解决方案的优劣。所以从一个基因组到其解的适应度形成一个映射。可以把遗传算法的过程看作是一个在多元函数里面求最优解的过程。可以这样想象，这个多维曲面里面有数不清的“山峰”，而这些山峰所对应的就是局部最优解。而其中也会有一个“山峰”的海拔最高的，那么这个就是全局最优解。而遗传算法的任务就是尽量爬到最高峰，而不是陷落在一些小山峰。（另外，值得注意的是遗传算法不一定要找“最高的山峰”，如果问题的适应度评价越小越好的话，那么全局最优解就是函数的最小值，对应的，遗传算法所要找的就是“最深的谷底”）

一个很有趣的例子

模拟物竞天择的生物进化过程，通过维护一个潜在解的群体执行了多方向的搜索，并支持这些方向上的信息构成和交换。是以面为单位的搜索，比以点为单位的搜索，更能发现全局最优解。（在遗传算法中，有很多袋鼠，它们降落到喜玛拉雅山脉的任意地方。这些袋鼠并不知道它们的任务是寻找珠穆朗玛峰。但每过几年，就在一些海拔高度较低的地方射杀一些袋鼠，并希望存活下来的袋鼠是多产的，在它们所处的地方生儿育女。）（或者换个说法。从前，有一大群袋鼠，它们被莫名其妙的零散地遗弃于喜马拉雅山脉。于是只好在那里艰苦的生活。海拔低的地方弥漫着一种无色无味的毒气，海拔越高毒气越稀薄。可是可怜的袋鼠们对此全然不觉，还是习惯于活蹦乱跳。于是，不断有袋鼠死于海拔较低的地方，而越是在海拔高的袋鼠越是能活得更久，也越有机会生儿育女。就这样经过许多年，这些袋鼠们竟然都不自觉地聚拢到了一个个的山峰上，可是在所有的袋鼠中，只有聚拢到珠穆朗玛峰的袋鼠被带回了美丽的澳洲。）

实现过程

遗传算法的实现过程实际上就像自然界的进化过程那样。首先寻找一种对问题潜在解进行“数字化”编码的方案。（建立表现型和基因型的映射关系）然后用随机数初始化一个种群（那么第一批袋鼠就被随意地分散在山脉上），种群里面的个体就是这些数字化的编码。接下来，通过适当的解码过程之后（得到袋鼠的位置坐标），用适应性函数对每一个基因个体作一次适应度评估（袋鼠爬得越高，越是受我们的喜爱，所以适应度相应越高）。用选择函数按照某种规定择优选择（我们要每隔一段时间，在山上射杀一些所在海拔较低的袋鼠，以保证袋鼠总体数目持平。）。让个体基因变异（让袋鼠随机地跳一跳）。然后产生子代（希望存活下来的袋鼠是多产的，并在那里生儿育女）。遗传算法并不保证你能获得问题的最优解，但是使用遗传算法的最大优点在于你不必去了解和操心如何去“找”最优解。（你不必去指导袋鼠向那边跳，跳多远。）而只要简单的“否定”一些表现不好的个体就行了。（把那些总是爱走下坡路的袋鼠射杀，这就是遗传算法的精粹！）

所以我们总结出遗传算法的一般步骤：

开始循环直至找到满意的解。

评估每条染色体所对应个体的适应度。
遵照适应度越高，选择概率越大的原则，从种群中选择两个个体作为父方和母方。
抽取父母双方的染色体，进行交叉，产生子代。
对子代的染色体进行变异。
重复2，3，4步骤，直到新种群的产生。

结束循环。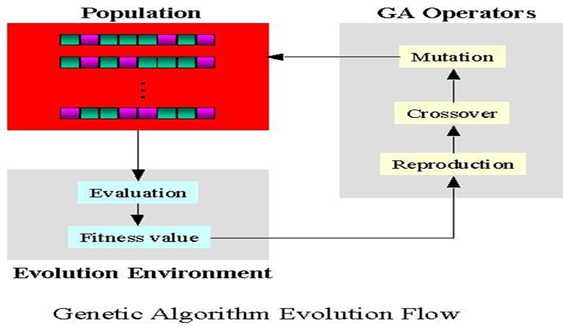

接下来，我们将详细地剖析遗传算法过程的每一个细节。

编制袋鼠的染色体—-基因的编码方式

受到人类染色体结构的启发，我们可以设想一下，假设目前只有“0”，“1”两种碱基，我们也用一条链条把他们有序的串连在一起，因为每一个单位都能表现出 1 bit的信息量，所以一条足够长的染色体就能为我们勾勒出一个个体的所有特征。这就是二进制编码法，染色体大致如下：

010010011011011110111110

上面的编码方式虽然简单直观，但明显地，当个体特征比较复杂的时候，需要大量的编码才能精确地描述，相应的解码过程（类似于生物学中的DNA翻译过程，就是把基因型映射到表现型的过程。）将过分繁复，为改善遗传算法的计算复杂性、提高运算效率，提出了浮点数编码。染色体大致如下：

1.2 –3.3 – 2.0 –5.4 – 2.7 – 4.3

（注：还有一种编码方式叫符号编码）

那么我们如何利用这两种编码方式来为袋鼠的染色体编码呢？因为编码的目的是建立表现型到基因型的映射关系，而表现型一般就被理解为个体的特征。比如人的基因型是46条染色体所描述的却能解码成一个眼，耳，口，鼻等特征各不相同的活生生的人。所以我们要想为“袋鼠”的染色体编码，我们必须先来考虑“袋鼠”的“个体特征”是什么。也许有的人会说，袋鼠的特征很多，比如性别，身长，体重，也许它喜欢吃什么也能算作其中一个特征。但具体在解决这个问题的情况下，我们应该进一步思考：无论这只袋鼠是长短，肥瘦，黑白只要它在低海拔就会被射杀，同时也没有规定身长的袋鼠能跳得远一些，身短的袋鼠跳得近一些。当然它爱吃什么就更不相关了。我们由始至终都只关心一件事情：袋鼠在哪里。因为只要我们知道袋鼠在那里，我们就能做两件必须去做的事情：

（1）通过查阅喜玛拉雅山脉的地图来得知袋鼠所在的海拔高度（通过自变量求适应函数的值。）以判断我们有没必要把它射杀。

（2）知道袋鼠跳一跳（交叉和变异）后去到哪个新位置。

如果我们一时无法准确的判断哪些“个体特征”是必要的，哪些是非必要的，我们常常可以用到这样一种思维方式：比如你认为袋鼠的爱吃什么东西非常必要，那么你就想一想，有两只袋鼠，它们其它的个体特征完全同等的情况下，一只长得黑，另外一只长得不是那么黑。你会马上发现，这不会对它们的命运有丝毫的影响，它们应该有同等的概率被射杀！只因它们处于同一个地方。（值得一提的是，如果你的基因编码设计中包含了袋鼠黑不黑的信息，这其实不会影响到袋鼠的进化的过程，而那只攀到珠穆朗玛峰的袋鼠黑与白什么的也完全是随机的，但是它所在的位置却是非常确定的。）

 **以上是对遗传算法编码过程中经常经历的思维过程，必须把具体问题抽象成数学模型，突出主要矛盾，舍弃次要矛盾。只有这样才能简洁而有效的解决问题。**

既然确定了袋鼠的位置作为个体特征，具体来说位置就是横坐标。那么接下来，我们就要建立表现型到基因型的映射关系。就是说如何用编码来表现出袋鼠所在的横坐标。由于横坐标是一个实数，所以说透了我们就是要对这个实数编码。回顾我们上面所介绍的两种编码方式，最先想到的应该就是，对于二进制编码方式来说，编码会比较复杂，而对于浮点数编码方式来说，则会比较简洁。恩，正如你所想的，用浮点数编码，仅仅需要一个浮点数而已。而下面则介绍如何建立二进制编码到一个实数的映射。

明显地，一定长度的二进制编码序列，只能表示一定精度的浮点数。譬如我们要求解精确到六位小数，由于区间长度为2 – (-1) = 3 ,为了保证精度要求，至少把区间[-1,2]分为3 × 106等份。又因为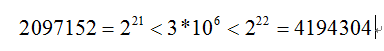

所以编码的二进制串至少需要22位。

把一个二进制串（b0,b1,….bn)转化位区间里面对应的实数值通过下面两个步骤。

（1）将一个二进制串代表的二进制数转化为10进制数：

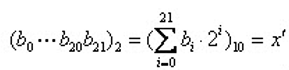
（2）对应区间内的实数：

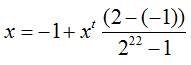
（像极了模数转换）

例如一个二进制串<1000101110110101000111>表示实数值0.637197。

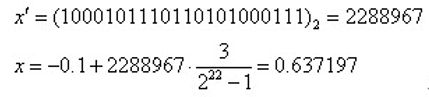
（纠正一个错误，这里是-1）

二进制串<0000000000000000000000>和<1111111111111111111111>则分别表示区间的两个端点值-1和2。

好了，目前为止我们把袋鼠的染色体给研究透了，让我们继续跟进袋鼠的进化旅程

物竞天择－－适应性评分与及选择函数。

物竞――适应度函数（fitness function）

自然界生物竞争过程往往包含两个方面：生物相互间的搏斗与及生物与客观环境的搏斗过程。但在我们这个实例里面，你可以想象到，袋鼠相互之间是非常友好的，它们并不需要互相搏斗以争取生存的权利。它们的生死存亡更多是取决于你的判断。因为你要衡量哪只袋鼠该杀，哪只袋鼠不该杀，所以你必须制定一个衡量的标准。而对于这个问题，这个衡量的标准比较容易制定：袋鼠所在的海拔高度。（因为你单纯地希望袋鼠爬得越高越好。）所以我们直接用袋鼠的海拔高度作为它们的适应性评分。即适应度函数直接返回函数值就行了。
天择――选择函数（selection）

自然界中，越适应的个体就越有可能繁殖后代。但是也不能说适应度越高的就肯定后代越多，只能是从概率上来说更多。（毕竟有些所处海拔高度较低的袋鼠很幸运，逃过了你的眼睛。）那么我们怎么来建立这种概率关系呢？下面我们介绍一种常用的选择方法――轮盘赌（Roulette Wheel Selection）选择法。

比如我们有5条染色体，他们所对应的适应度评分分别为：5，7，10，13，15

所以累计总适应度为：

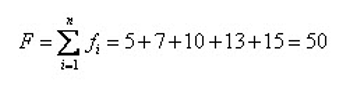
所以各个个体被选中的概率分别为：

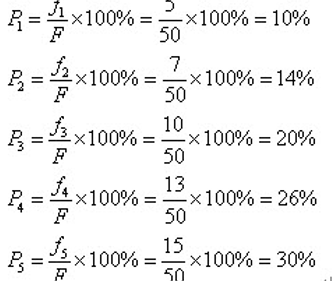
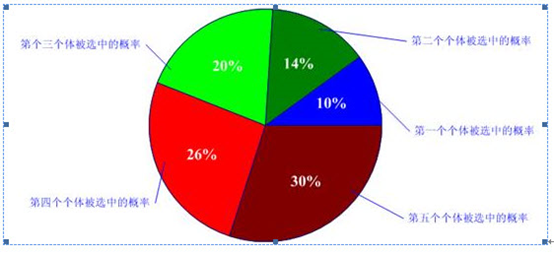
你可以想象一下，我们转动轮盘，轮盘停下来的时候，指针会随机地指向某一个个体所代表的区域，那么非常幸运地，这个个体被选中了。（很明显，适应度评分越高的个体被选中的概率越大。）

注：还有精英选择机制

遗传变异――基因重组（交叉）与基因突变。

应该说这两个步骤就是使得子代不同于父代的根本原因（注意，我没有说是子代优于父代，只有经过自然的选择后，才会出现子代优于父代的倾向。）。对于这两种遗传操作，二进制编码和浮点型编码在处理上有很大的差异，其中二进制编码的遗传操作过程，比较类似于自然界里面的过程，下面将分开讲述。

1.基因重组/交叉(recombination/crossover)

（1）二进制编码

二进制编码的基因交换过程非常类似高中生物中所讲的同源染色体的联会过程――随机把其中几个位于同一位置的编码进行交换，产生新的个体。

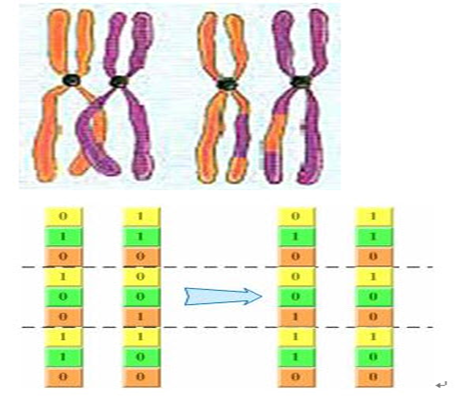
（2）浮点数编码

如果一条基因中含有多个浮点数编码，那么也可以用跟上面类似的方法进行基因交叉，不同的是进行交叉的基本单位不是二进制码，而是浮点数。而如果对于单个浮点数的基因交叉，就有其它不同的重组方式了，比如中间重组：随机产生就能得到介于父代基因编码值和母代基因编码值之间的值作为子代基因编码的值。比如5.5和6交叉，产生5.7，5.6。

考虑到“袋鼠跳”问题的具体情况――袋鼠的个体特征仅仅表现为它所处的位置。可以想象，同一个位置的袋鼠的基因是完全相同的，而两条相同的基因进行交叉后，相当于什么都没有做，所以我们不打算在这个例子里面使用交叉这一个遗传操作步骤。（当然硬要这个操作步骤也不是不行的，你可以把两只异地的袋鼠捉到一起，让它们交配，然后产生子代，再把它们送到它们应该到的地方。）

2.基因突变(Mutation)

（1）二进制编码

 基因突变过程：基因突变是染色体的某一个位点上基因的改变。基因突变使一个基因变成它的等位基因，并且通常会引起一定的表现型变化。正如上面所说，二进制编码的遗传操作过程和生物学中的过程非常相类似，基因串上的“ 0”或“ 1”有一定几率变成与之相反的“ 1”或“ 0”。例如下面这串二进制编码：

101101001011001

经过基因突变后，可能变成以下这串新的编码：

001101011011001

（2）浮点型编码

浮点型编码的基因突变过程一般是对原来的浮点数增加或者减少一个小随机数。比如原来的浮点数串如下：

1.2,3.4,5.1, 6.0, 4.5

变异后，可能得到如下的浮点数串：

1.3,3.1,4.9, 6.3, 4.4

当然，这个小随机数也有大小之分，我们一般管它叫“步长”。（想想“袋鼠跳”问题，袋鼠跳的长短就是这个步长。）一般来说步长越大，开始时进化的速度会比较快，但是后来比较难收敛到精确的点上。而小步长却能较精确的收敛到一个点上。所以很多时候为了加快遗传算法的进化速度，而又能保证后期能够比较精确地收敛到最优解上面，会采取动态改变步长的方法。其实这个过程与前面介绍的模拟退火过程比较相类似。

到此为止，基因编码，基因适应度评估，基因选择，基因变异都一一实现了，剩下来的就是把这些遗传过程的“零件”装配起来了。（写成代码）
总结：

编码原则
完备性（completeness）：问题空间的所有解都能表示为所设计的基因型；
健全性（soundness）：任何一个基因型都对应于一个可能解；
非冗余性（non-redundancy）：问题空间和表达空间一一对应。

适应度函数的重要性
适应度函数的选取直接影响遗传算法的收敛速度以及能否找到最优解。一般而言，适应度函数是由目标函数变换而成的。

适应度函数设计不当有可能出现欺骗问题：
（1）进化初期，个别超常个体控制选择过程；
（2）进化末期，个体差异太小导致陷入局部极值。

欺骗问题举例：

还是袋鼠问题，如果低海拔的地方出现毒雾，会杀死袋鼠，只有爬上珠穆朗玛峰顶端的袋鼠才能生存下来。

因为喜马拉雅山脉有很多山峰，我们以高度作为适应度，case（1）：如果不在珠峰的猴子若比在珠峰半山腰的猴子要高，因为种群大小不变，在珠峰的猴子可能就会被淘汰；case（2）：100只猴子都不在珠峰；