数据结构&算法相关知识总结

Posted on Edited on In

learn algorithm

Algorithm1

week1

主要讲了 Union-find 算法

这里复习一下并且把作业给写了

Course

dynamic connectivity

看了HW怎么感觉啥都没学 呜呜呜

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
import edu.princeton.cs.algs4.UF;

public class eg1 {
    public static void main(String[] args) {
        int N = StdIn.readInt();
        UF uf = new UF(N);
        while (!StdIn.isEmpty()) {
            int p = StdIn.readInt();
            int q = StdIn.readInt();
            if (!uf.connected(p, q)) {
                uf.union(p, q);
                StdOut.println(p + " " + q);
            }
        }
    }
}

啥也不是 就讲了 UF 类的一些操作 和 StdIn StdOut 怎么用

quick find

因为我们的目的是找到那几部分是连接起来的 所以我们可以采取这种方法

先建一个如下的数组

image-20221018144352678

看下面这张图

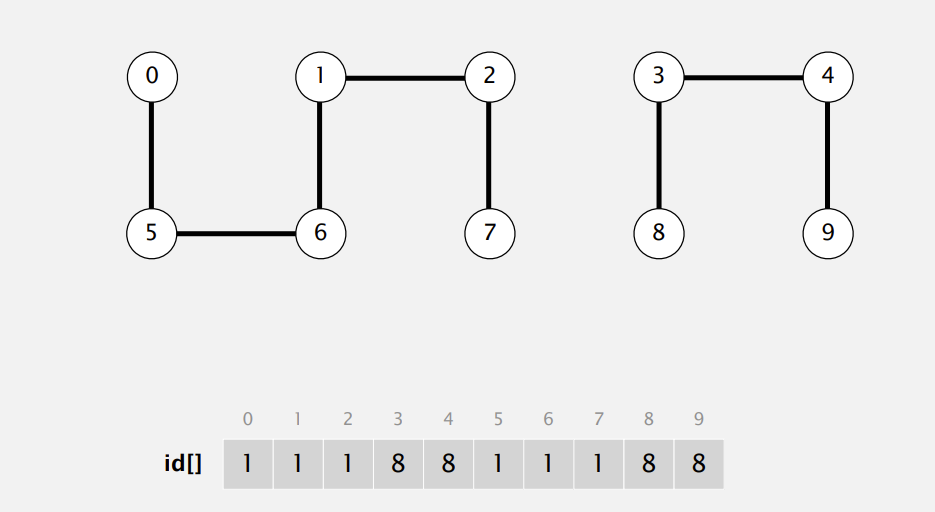
image-20221018144254213

如果我们 union(3,4) 就把 3,4 都改成3 或都改成4（但我们图中都改成第二个参数的值 即4）

接下来我们 来连 4,9 的时候 就也向之前那样 于是位置3,4,9都变成了 9

之后再连上 8 于是 3,4,8,9 位置的值都变成了 8

最终 我们得到的值只有 1,8 也就是得到了两部分

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class QuickFindUF {
    private int[] id;
    
	//建立一个数组 id 与 值 相对应
    public QuickFindUF(int N) {
        id = new int[N];
        for (int i = 0; i < N; i++)
            id[i] = i;
    }
	
    // 判断两点是否连接 的方法就是这两点的值是否相等
    public boolean connected(int p, int q) {
        return id[p] == id[q];
    }

    // 改之前已经连起来的值  但这里复杂度为N方
    public void union(int p, int q) {
        int pid = id[p];
        int qid = id[q];
        for (int i = 0; i < id.length; i++)
            if (id[i] == pid) id[i] = qid;
    }
}

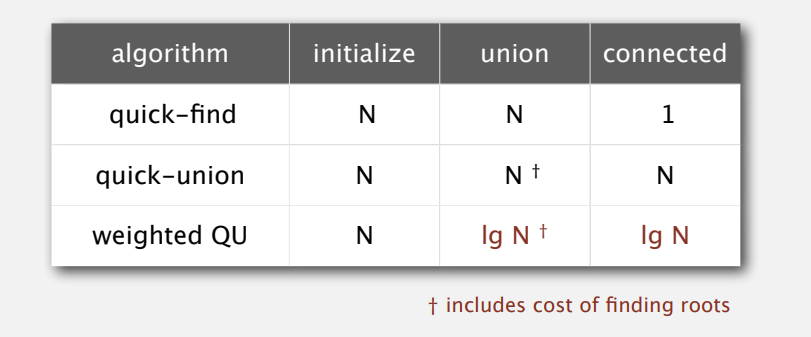
缺点 太慢 需要 N方的复杂度来执行

image-20221018145111296

quick union

来看看 quick-union 这样做的好处是 设置两点union的时候不用把之前串起来的全改一遍

只需要改动一次 那这样union的复杂度就下降到了N 但是貌似查起来就费力一点

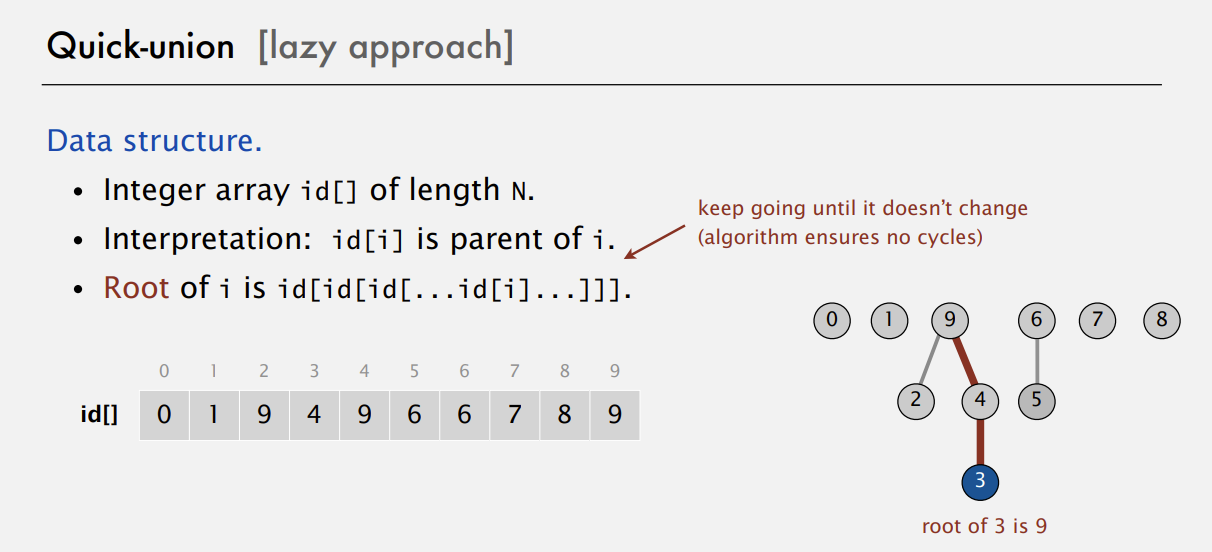
image-20221018145458506

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class QuickUnionUF
{
    private int[] id;
    public QuickUnionUF(int N)
    {
        id = new int[N];
        for (int i = 0; i < N; i++) id[i] = i;
    }
    private int root(int i)
    {
        while (i != id[i]) i = id[i];
        return i;
    }
    public boolean connected(int p, int q)
    {
        return root(p) == root(q);
    }
    public void union(int p, int q)
    {
        int i = root(p);
        int j = root(q);
        id[i] = j;
    }
}

判断相不相等就是找root是不是一样 那如何找root呢？我们可以轻松地发现 root点 的index和值总是相等的 所以判断一个点的最终root是谁 只需要按他的值网上去找 直到index==index.data 即可

ok 让我们现在再来看一看复杂度！很好 我们的 union 只需要在 长度为N的数组上做N次了！

image-20221018150047592

接下来让我们来看看这两种方法分别的优缺点

image-20221018150416503

ok 我们接下来要处理 trees 太深的缺点

improvements 1: weighting

争取能用我自己的语言描述清楚 总的来说就是一句话

小树 -> 放到大树下面 （如果相同就随意放

这里的小和大指的是树的deep

所以要实现这种算法 免不了

  • 计算树的深度
  • 找 root 节点
  • 比较树的深度

code

Find. Identical to quick-union.

还是判断他们最高的root想不想同

1
return root(p) == root(q);

union

如果俩点已经在一个root下的树中 说明他们已经是相连的了

否则 将小树总root改为大树的总root 然后将记录其高度的值改为和大树一样

1
2
3
4
5
int i = root(p);
int j = root(q);
if (i == j) return;
if (sz[i] < sz[j]) { id[i] = j; sz[j] += sz[i]; }
else { id[j] = i; sz[i] += sz[j]; }

想想为啥都变 lg N 了呢？以为有部分已经自动连上了 但这里我也说不太清楚

image-20221018152134449

Improvement 2: path compression

啥意思 看图就明白了

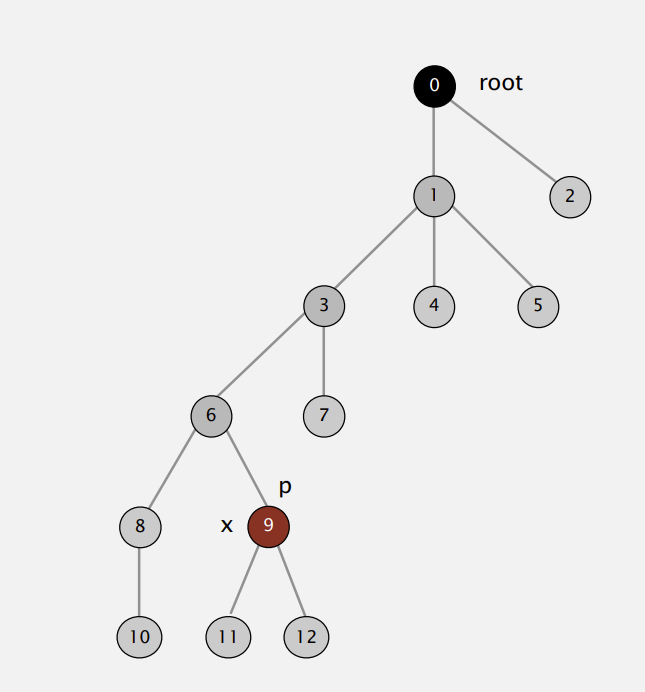
image-20221018153710329

也就是把树给他展开 直连root

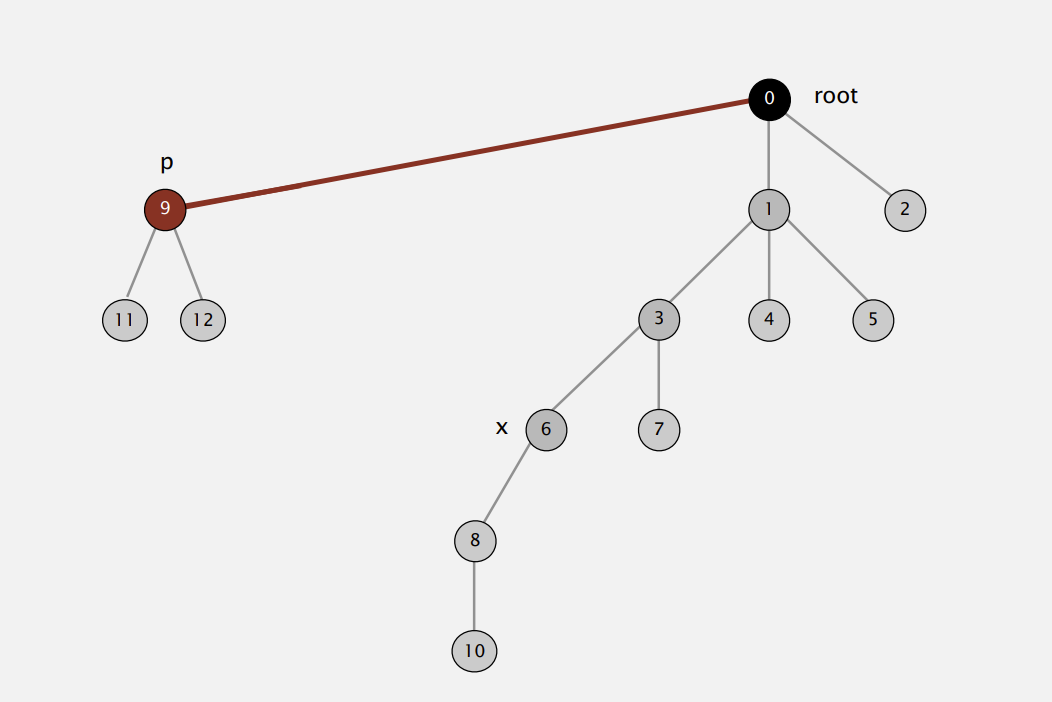
image-20221018153740653

而实现这个只需要加一行代码

1
2
3
4
5
6
7
8
9
private int root(int i)
{
	while (i != id[i])
 	{
 		id[i] = id[id[i]];
 		i = id[i];
 	}
	return i;
}

奶思！

然后prof说这个两种可能在应用中一样好 至于如何证明 超出了本课程的范围

HW

HW1

Write a program to estimate the value of the percolation threshold via Monte Carlo simulation.

简单来说就是看看你能不能想办法来写个 算法来判断上下部能不能连通？

好像有点小难

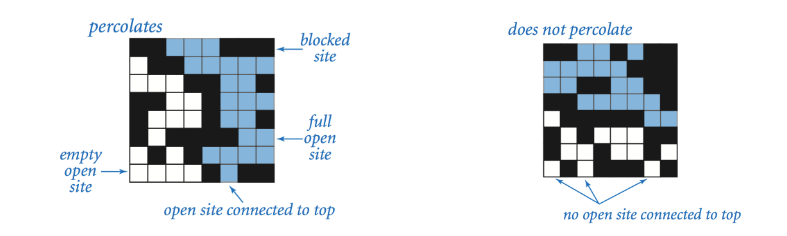
image-20221018135548373

总的解决方案：

  • 先做这样一个标记 对应每个点

image-20221018155330351

  • 在上下端虚拟出一个点 然后用我们之前学的并查集方法判断他们是否连通！

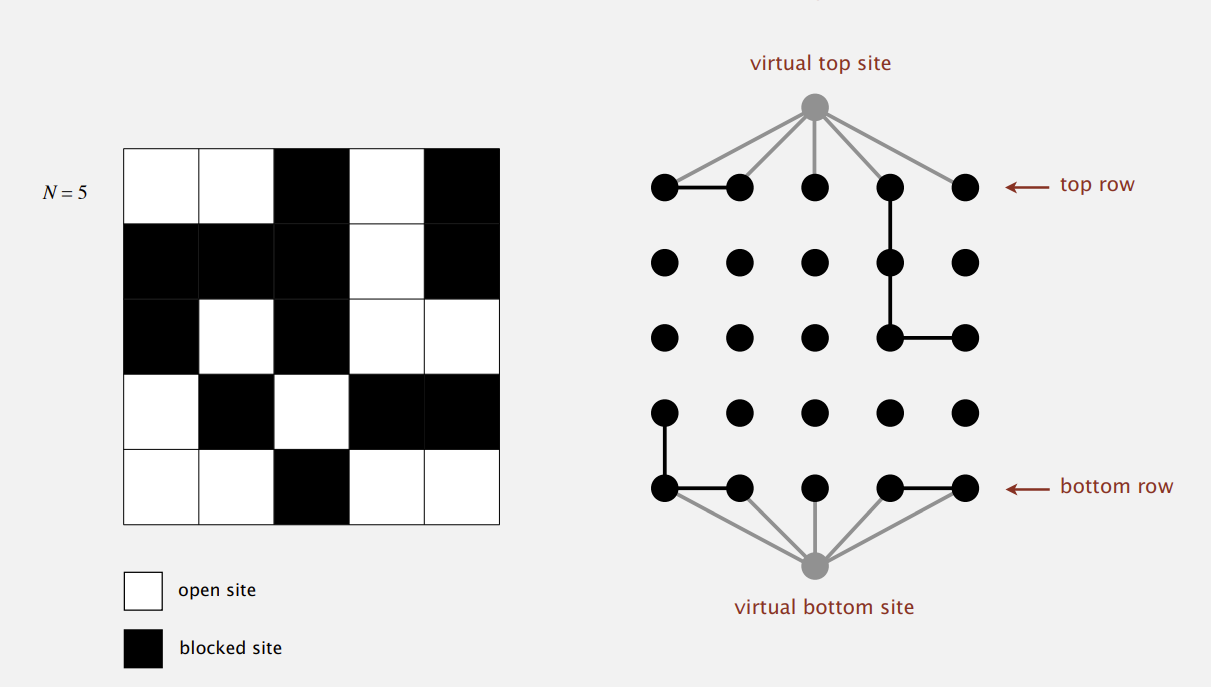
image-20221018155426432

要实现这些接口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class Percolation {

    // creates n-by-n grid, with all sites initially blocked
    public Percolation(int n)

    // opens the site (row, col) if it is not open already
    public void open(int row, int col)

    // is the site (row, col) open?
    public boolean isOpen(int row, int col)

    // is the site (row, col) full?
    public boolean isFull(int row, int col)

    // returns the number of open sites
    public int numberOfOpenSites()

    // does the system percolate?
    public boolean percolates()

    // test client (optional)
    public static void main(String[] args)
}

整理完有点累了 今天不一定能写完，，，

之前的方法都是包装好的直接调用就行o.o

image-20221019190739154

week2

数据结构

树

红黑树

老婆的讲解

性质

  1. 节点是红色或黑色 （怎么感觉想废话
  2. 根节点是黑色
  3. 叶子结点（最底层不存放数据的节点），都是黑色，且都为空
  4. 红色节点的父节点and子节点都为黑色（不会存在两个连续的红色节点）
  5. 从任一节点到叶子节点的所有路径都包含相同数量的黑色节点

红黑树和234树等价