跟run哥一起学PCA

Posted on Edited on In

看看PCA

https://www.bilibili.com/video/BV1E5411E71z/?spm_id_from=333.337.search-card.all.click&vd_source=a2c222cd47523aaf38b1191c9089cd79

What is PCA?

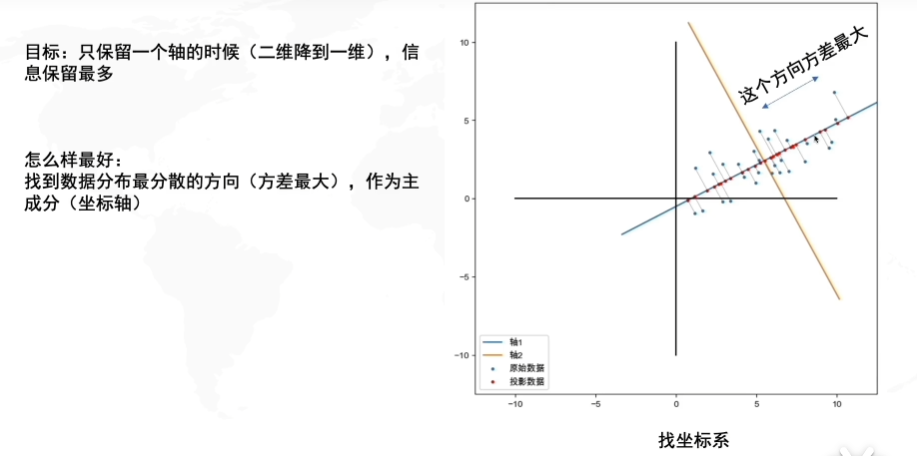
PCA的目的就是找到一个坐标系，使得数据在只保留一个维度的时候，信息损失是最小的。

image-20221221180518147

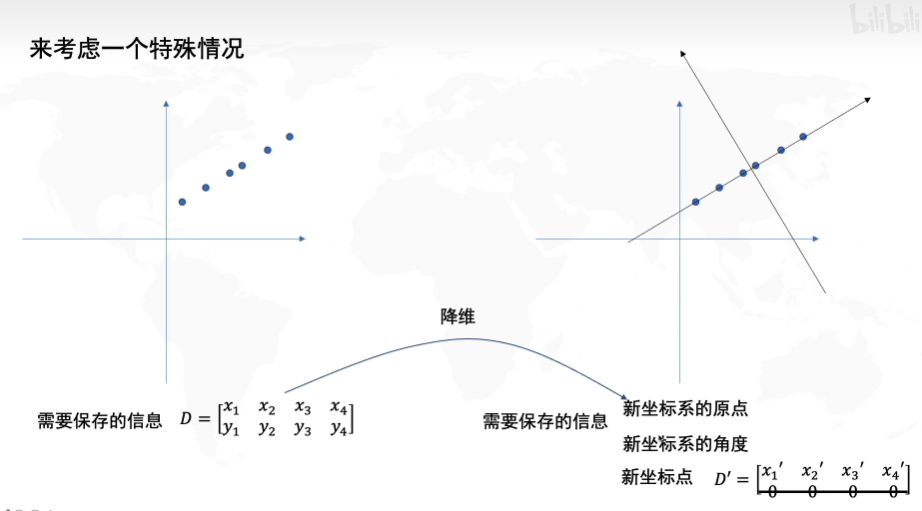
首先：去中心化（把坐标原点放在数据中心）

然后：找坐标系（找到哦啊方差最大的方向）

问题是：怎么找到方差最大的方向

image-20221221180809571

为什么要做PCA

为什么要做主成分分析
在很多场景中需要对多变量数据进行观测，在一定程度上增加了数据采集的工作量。更重要的是：多变量之间可能存在相关性，从而增加了问题分析的复杂性。

如果对每个指标进行单独分析，其分析结果往往是孤立的，不能完全利用数据中的信息，因此盲目减少指标会损失很多有用的信息，从而产生错误的结论。

因此需要找到一种合理的方法，在减少需要分析的指标同时，尽量减少原指标包含信息的损失，以达到对所收集数据进行全面分析的目的。由于各变量之间存在一定的相关关系，因此可以考虑将关系紧密的变量变成尽可能少的新变量，使这些新变量是两两不相关的，那么就可以用较少的综合指标分别代表存在于各个变量中的各类信息。主成分分析与因子分析就属于这类降维算法。

伪代码

image-20221221195737311

https://gitee.com/ni1o1/pygeo-tutorial/blob/master/12-.ipynb

协方差

image-20221221202711404

算一手相关性

1
2
3
4
5
6
# 定义一个函数，输入X，Y能得到X，Y之间的协方差
def getcov(X,Y):

    covxy = ((X-X.mean())*(Y-Y.mean())).sum()/(len(X)-1)

    return covxy

numpy实现

1
C = np.cov(data_norm.T)

计算协方差矩阵的特征向量和特征值

image-20221221204059934

1
2
3
4
5
#计算特征值和特征向量
vals, vecs = np.linalg.eig(C)
#重新排序，从大到小
vecs = vecs[:,np.argsort(-vals)]
vals = vals[np.argsort(-vals)]

协方差矩阵的特征向量就是R

计算投影

1
2
3
4
5
#数据在主成分1上的投影坐标是Y
k=1
Q = vecs[:,:k]
Y = np.matmul(data_norm,Q)
Y

最近重构性和最大可分性的思路

参考

https://blog.csdn.net/weixin_43312354/article/details/105653308

https://blog.csdn.net/a8039974/article/details/81285238